Bu makale de gene email üzerinden aldığım bir soruyu cevaplayacağım.

Soru, C# ile Binary Search Tree örneği nasıl geliştirebilirim?

Önce Tree (Ağaç) yapılarını inceleyelim.

Tree (Ağaç) yapıları ile, birbirleri arasında Parent-Child ilişkisi bulunan veriler modellenebiliyor.

Örneğin, bilgisayardaki dizinler ve dosyalar, ürün ağaçları, veya organizasyon şemaları, Tree (Ağaç) yapısında saklanırlar;

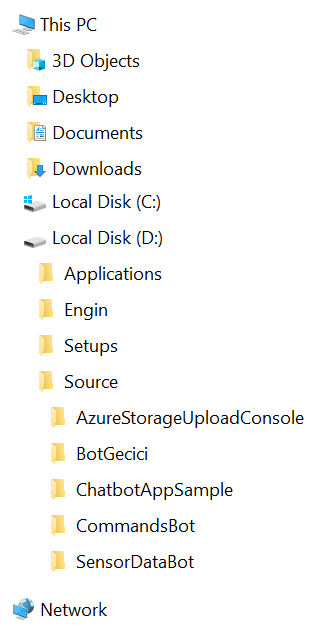
Tree (Ağaç) yapılarında, bir öğenin birden fazla alt öğesi olabilir

Hatta Root (Kök) öğe bile, gerekirse birden fazla olabilir.

Tree (Ağaç) veri yapılarına ilişkin tanımlamalar;

• Root (Kök)
  Ağacın başlangıç node'udur
• Node (Düğüm)
  Ağacın her bir node'una verilen isimdir
• Child (Çocuk)
  Bir node'a bağlı olan node'lara verilen isimdir
• Parent (Aile)
  Node'ların bağlı olduğu node'a verilen isimdir
• Sibling (Kardeş)
  Aynı node'a bağlı olan node'lara verilen isimdir
• Degree (Derece)
  Bir node'dan başlayarak en alt node'a gidene kadar geçilen katman sayıdır
• Path (Yol)
  Bir node'a varabilmek için izlenmesi gereken yola verilen isimdir

Binary Tree (genellikle İkili Ağaç olarak Türkçeleştirilir) yapıları ise, Root (Kök) olarak tek bir elemana sahip olan ve her dalında en fazla 2 öğe bulunabilen özel bir Tree (Ağaç) veri modelidir.

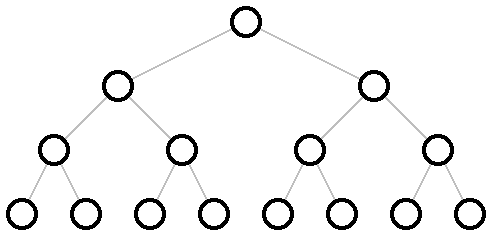
Gelelim asıl konumuza, Binary Search Tree :)

Binary Search Tree yapıları, Binary Tree yapılarının özelleşmiş bir halidir.

Root (Kök) olarak gene tek bir node‘a sahiptir, her node, kendisine bağlı en fazla 2 node‘a sahip olabilir.

Bu noktaya kadar Binary Tree yapıları ile aynı özelliklere sahip, farklı olarak, node‘lara bağlanan child node‘ların içerdiği değerler, parent node‘un kendi değerinden küçükse soldaki, büyük veya eşitse sağdaki node‘a kaydedilir.

Böylece, Tree (Ağaç) yapısı üzerinde yapılacak aramalar çok hızlı sonuçlanacaktır.

Tree (Ağaç) yapısının Degree (Derece) değeri kaç ise, o kadar adımda aranan değere ulaşılabilir.

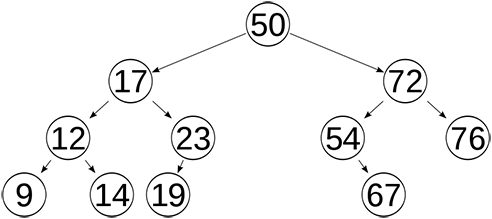
Yukarıdaki örnekte, 50 değerine 1 adımda, 72 değerine 2 adımda, 23 değerine 3 adımda, 67 değerine 4 adımda ulaşılabilecektir.

Binary Search Tree yapıları sayesinde, int.Max (2^32 : 2.147.483.647) kadar farklı değere sahip olan Tree (Ağaç) yapılarında bile arama işlemi 32 adımda sonuçlanacaktır.

.Net Core ile Binary Search Tree örneği geliştirmek için hemen yeni bir proje oluşturalım;

İlk olarak Node sınıfını oluşturalım. Nispeten basit bir sınıf olacak;

Value özelliği sayesinde int tipinde değer içerebiliyor, ayrıca kendisine bağlanabilecek 2 Node‘u, Left ve Right isimli özelliklerde tutabiliyor.

Fakat int yerine string, DateTime veya Customer tipli Node‘lar oluşturmak istersek yeni Node sınıfları üretmemiz gerekir.

Daha iyisi, Node sınıfını Generic hale getirmek;

Artık Tree sınıfını yazabiliriz ve onu da Generic yapmakta fayda var;

Tree sınıfına yazdığımız Top özelliği sayesinde, Tree (Ağaç) yapısının başlangıç Node‘unu tanımlamış olduk.

Aslında Binary Search Tree yapısını tamamlamış olduk. Fakat yeni Node eklemek, hatta ekranda listelemek için gereken method’ları da Tree sınıfına eklememiz iyi olacaktır.

Node eklemek için Tree sınıfına Add() methodu ekleyelim.

Add() methodu parametre olarak T tipinde değer alsın ve bu değere uygun bir yer bulup ekleme işlemini gerçekleştirsin.

Hatta, Add() sınıfının T tipinde parametresini dizi şeklinde yapalım, böylece, istenirse aynı anda birden fazla değer ekleme işlemine tabi tutulabilir.

Hatta, T[] tipindeki parametrenin başına params anahtar kelimesini ekleyebiliriz ve böylece Add() methodu çağırılırken değerler dizi şeklinde değil, virgülle ayrılmış şekilde de verilebilir.

Binary Search Tree yapısına ekleyeceğimiz Node‘ları, mümkün olduğu kadar dengelememiz iyi olacaktır. Böylece, arama işlemi çok hızlı gerçekleşir.

Dengeli dağıtılan Node yapısına Balanced Tree adı verilir.

Eğer dengeli bir ağaç yapısı oluşturamazsak, Node‘lar sağlı-sollu değil, uç-uca dizilecektir.

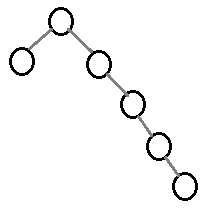
Uç-Uca dizilen Node‘lar üzerinde arama yapılacağı zaman Root (Kök) Node‘dan başlanıp, neredeyse tüm Node’lara uğranması gerekir.

Dengeli dizilen Node‘lar üzerinde arama yapılacağı zaman ise, Root (Kök) Node‘dan başlandığında, her seferinde ya Left Node, ya Right Node üzerinden devam edilerek, çok daha az Node‘a uğranır.

Binary Search Tree yapısını Balanced (Dengeli) hale getirmek için, ekleyeceğimiz Node‘ların tam orta noktasını Root (Kök) Node olarak belirlemeliyiz.

Add() methodunun içerisinde, parametre olarak gelen dizinin orta noktasını bulmak için, önce sıralıyor, sonra dizi uzunluğunun yarısı kadar elemanı atlıyor, karşımıza çıkan ilk elemanı seçiyoruz;

Orta elemanı diziden çıkartıp, dizinin ilk elemanı olacak şekilde tekrar Insert() ediyoruz.

Artık dizi üzerinde bir döngü kurup, tüm Node‘ları tek tek oluşturabiliriz;

Burada dikkat edilmesi gereken noktalar,

• Top özelliğine dizinin ilk kaydını (dizinin orta elemanı aslında) vermemiz
• Döngünün her iteration'ında dizi elemanını Tree'nin Node'ları ile karşılaştırıyoruz
• Comparer<T> sınıfının Default özelliğinde yer alan Compare methodu ile karşılaştırma yapıyoruz
• Eğer karşılaştırma sonucunda -1 değerini elde ediyorsak, daha küçük, 0 elde ediyorsak eşit, 1 elde ediyorsak daha büyük demektir
• Karşılaştırma sonucuna göre ya Left ya da Right özelliği üzerinden ilerleyerek, Tree'ye Node eklemesi yapıyoruz